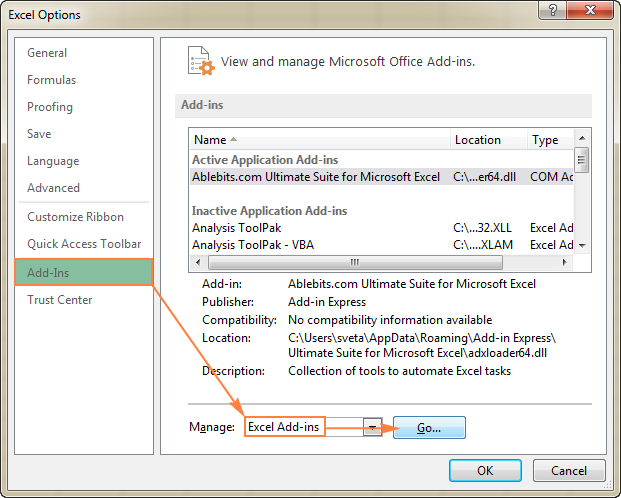
With the Analysis Tool Pak installed, you now can perform regression analysis by clicking on the “Regression” option from the “Data Analysis” window. For Excel 2010, go to the backstage view of Excel and click “Add-Ins.” In the bottom of the window that opens, you should see “Manage” with “Excel Add-Ins” chosen. In order to perform a regression analysis we choose from the Microsoft Excel menu.: Tools Data analysis Regression Note that data analysis tool should have been previously added to Microsoft Excel during the program setup (Tools – Add-Ins – Analysis ToolPak). The pop-up input dialog box is shown on Fig.1. Multiple Linear Regression Excel 2010 Tutorial For use with more than one quantitative independent variable This tutorial combines information on how to obtain regression output for Multiple Linear Regression from Excel (when all of the variables are quantitative) and some aspects of understanding what the output is telling you. How to do regression analysis in Excel 2011 (Mac) - since there is no Microsoft Toolpak add-in or plug-in. Steps to setup, start and use StatPlus, the free s. Regression analysis in Excel - the basics In statistical modeling, regression analysis is used to estimate the relationships between two or more variables: Dependent variable (aka criterion variable) is the main factor you are trying to understand and predict.
- Regression Analysis Excel 2010 Macros
- Excel Data Analysis Regression Tool
- Understanding Regression Analysis In Excel
There is a lot more to the Excel Regression output than just the regression equation. If you know how to quickly read the output of a Regression done in, you’ll know right away the most important points of a regression: if the overall regression was a good, whether this output could have occurred by chance, whether or not all of the independent input variables were good predictors, and whether residuals show a pattern (which means there’s a problem).
Excel Regression Output With Color-Coding Added
This video will illustrate exactly how to quickly and easily understand the output of Regression performed in Excel:
Step-By-Step Video About How To Quickly Read and Understand the Output of Excel Regression
(Is Your Sound and Internet Connection Turned On?)
Amazon Kindle Users Click here to View Video
The 4 Most Important Parts of Regression Output
1) Overall Regression Equation’s Accuracy
(R Square and Adjusted R Square)
2) Probability That This Output Was Not By Chance
(ANOVA – Significance of F)
3) Individual Regression Coefficient and Y-Intercept Accuracy
4) Visual Analysis of Residuals
Some parts of the Excel Regression output are much more important than others. The goal here is for you to be able to glance at the Excel Regression output and immediately understand it, so we will focus our attention only on the four most important parts of the Excel regression output.
1) Overall Regression’s Accuracy
R Square
This is the most important number of the output. R Square tells how well the regression line approximates the real data. This number tells you how much of the output variable’s variance is explained by the input variables’ variance. Ideally we would like to see this at least 0.6 (60%) or 0.7 (70%).
Adjusted R Square
This is quoted most often when explaining the accuracy of the regression equation. Adjusted R Square is more conservative the R Square because it is always less than R Square. Another reason that Adjusted R Square is quoted more often is that when new input variables are added to the Regression analysis, Adjusted R Square increases only when the new input variable makes the Regression equation more accurate (improves the Regression equation’s ability to predict the output). R Square always goes up when a new variable is added, whether or not the new input variable improves the Regression equation’s accuracy.
2) Probability That This Output Was Not By Chance
Significance of F
This indicates the probability that the Regression output could have been obtained by chance. A small Significance of F confirms the validity of the Regression output. For example, if Significance of F = 0.030, there is only a 3% chance that the Regression output was merely a chance occurrence.
3) Individual Regression Coefficient Accuracy
P-value of each coefficient and the Y-intercept
The P-Values of each of these provide the likelihood that they are real results and did not occur by chance. The lower the P-Value, the higher the likelihood that that coefficient or Y-Intercept is valid. For example, a P-Value of 0.016 for a regression coefficient indicates that there is only a 1.6% chance that the result occurred only as a result of chance.
4) Visual Analysis of Residuals
Charting the Residuals
The Residual Chart
The residuals are the difference between the Regression’s predicted value and the actual value of the output variable. You can quickly plot the Residuals on a scatterplot chart. Look for patterns in the scatterplot. The more random (without patterns) and centered around zero the residuals appear to be, the more likely it is that the Regression equation is valid.
There are many other pieces of information in the Excel regression output but the above four items will give a quick read on the validity of your Regression.
Multiple linear regression is a method we can use to understand the relationship between two or more explanatory variables and a response variable.
This tutorial explains how to perform multiple linear regression in Excel.
Note: If you only have one explanatory variable, you should instead perform simple linear regression.
Example: Multiple Linear Regression in Excel
Suppose we want to know if the number of hours spent studying and the number of prep exams taken affects the score that a student receives on a certain college entrance exam.
To explore this relationship, we can perform multiple linear regression using hours studied and prep exams taken as explanatory variables and exam score as a response variable.
Perform the following steps in Excel to conduct a multiple linear regression.
Step 1: Enter the data.
Enter the following data for the number of hours studied, prep exams taken, and exam score received for 20 students:
Step 2: Perform multiple linear regression.
Along the top ribbon in Excel, go to the Data tab and click on Data Analysis. If you don’t see this option, then you need to firstinstall the free Analysis ToolPak.
Once you click on Data Analysis, a new window will pop up. Select Regression and click OK.
For Input Y Range, fill in the array of values for the response variable. For Input X Range, fill in the array of values for the two explanatory variables. Check the box next to Labels so Excel knows that we included the variable names in the input ranges. For Output Range, select a cell where you would like the output of the regression to appear. Then click OK.
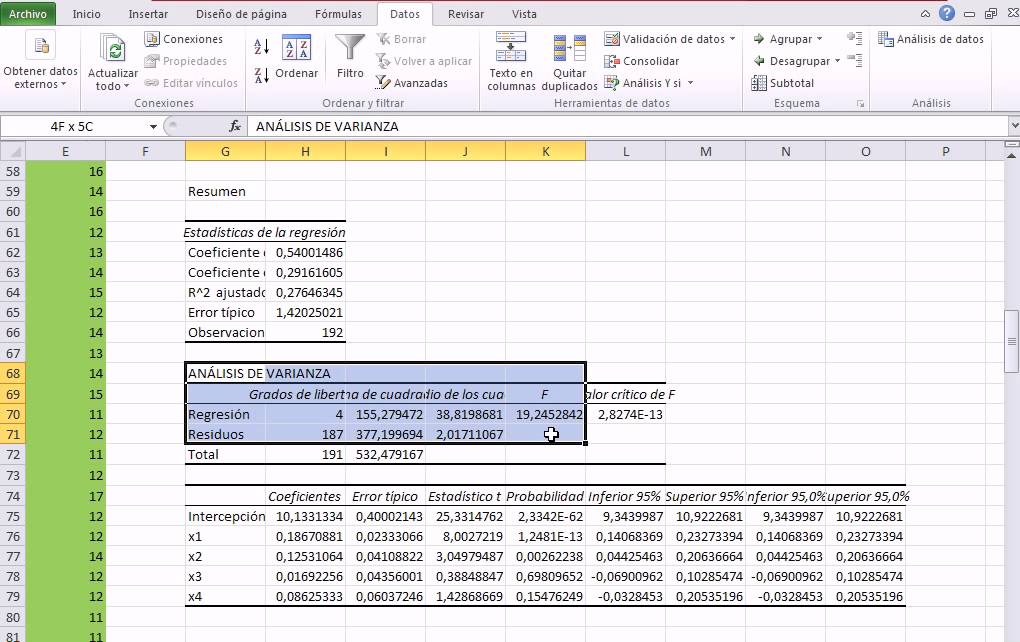
The following output will automatically appear:
Step 3: Interpret the output.
Here is how to interpret the most relevant numbers in the output:
R Square: 0.734. This is known as the coefficient of determination. It is the proportion of the variance in the response variable that can be explained by the explanatory variables. In this example, 73.4% of the variation in the exam scores can be explained by the number of hours studied and the number of prep exams taken.
Standard error:5.366. This is the average distance that the observed values fall from the regression line. In this example, the observed values fall an average of 5.366 units from the regression line.
F: 23.46. This is the overall F statistic for the regression model, calculated as regression MS / residual MS.
Significance F: 0.0000. This is the p-value associated with the overall F statistic. It tells us whether or not the regression model as a whole is statistically significant. In other words, it tells us if the two explanatory variables combined have a statistically significant association with the response variable. In this case the p-value is less than 0.05, which indicates that the explanatory variables hours studied and prep exams taken combined have a statistically significant association with exam score.
P-values. The individual p-values tell us whether or not each explanatory variable is statistically significant. We can see that hours studied is statistically significant (p = 0.00) while prep exams taken (p = 0.52) is not statistically signifciant at α = 0.05. Since prep exams taken is not statistically significant, we may end up deciding to remove it from the model.
Coefficients: The coefficients for each explanatory variable tell us the average expected change in the response variable, assuming the other explanatory variable remains constant. For example, for each additional hour spent studying, the average exam score is expected to increase by 5.56, assuming that prep exams taken remains constant.
Here’s another way to think about this: If student A and student B both take the same amount of prep exams but student A studies for one hour more, then student A is expected to earn a score that is 5.56 points higher than student B.
We interpret the coefficient for the intercept to mean that the expected exam score for a student who studies zero hours and takes zero prep exams is 67.67.
Estimated regression equation: We can use the coefficients from the output of the model to create the following estimated regression equation:
exam score = 67.67 + 5.56*(hours) – 0.60*(prep exams)
We can use this estimated regression equation to calculate the expected exam score for a student, based on the number of hours they study and the number of prep exams they take. For example, a student who studies for three hours and takes one prep exam is expected to receive a score of 83.75:
exam score = 67.67 + 5.56*(3) – 0.60*(1) = 83.75
Regression Analysis Excel 2010 Macros
Keep in mind that because prep exams taken was not statistically significant (p = 0.52), we may decide to remove it because it doesn’t add any improvement to the overall model. In this case, we could perform simple linear regression using only hours studied as the explanatory variable.
The results of this simple linear regression analysis can be found here.
Additional Resources
Once you perform multiple linear regression, there are several assumptions you may want to check including:
Excel Data Analysis Regression Tool
1.Testing for multicollinearity using VIF.
Understanding Regression Analysis In Excel
2. Testing for heterodscedasticity using a Breusch-Pagan test.
3. Testing for normality using a Q-Q plot.
